Geodesic distance between probability distributions is not the KL divergence
11 Jul 2017Ever wondered how to measure distance between probability distributions? Statistical distance article on Wikipedia gives more than 10 different definitions. Why so many and which one to use? In this post, we will try to develop some geometric intuition to bring order into this diversity.
For simplicity, let’s consider a discrete probability distribution over two elements $p = [p_1, p_2]$. We can view $p$ as a vector in $\mathbb{R}^2$ lying on the standard simplex $\Delta^1$. We could measure distance between distributions as distance between points on the simplex. One should however be careful as to what metric tensor to use on that space.
Metric induced from the sphere
Consider a sphere $x_1^2 + x_2^2 = 1$ embedded in $\mathbb{R}^2$. Non-linear transformation $p_i = x_i^2$ turns the sphere into a simplex $p_1 + p_2 = 1$. The distance on the sphere is the arc length. Question: What is the distance on the simplex after such a transformation? Following the Fisher metric article, let’s denote the Euclidean metric by $h = dx_1^2 + dx_2^2$. Substituting $x_i = \sqrt{p_i}$, we obtain
\begin{equation} \label{metric} h = (d\sqrt{p_1})^2 + (d\sqrt{p_2})^2 = \frac{1}{4}\frac{dp_1^2}{p_1} + \frac{1}{4}\frac{dp_2^2}{p_2} = \frac{1}{4}\sum_i \frac{dp_i^2}{p_i}. \end{equation}
Note that $dp_1 = -dp_2$ and $p_2 = 1 - p_1$, therefore $h$ simplifies to
The Fisher metric is usually defined without the $1/4$ coefficient, i.e.,
where subscript $p$ denotes the point at which the metric tensor is computed.
Geodesic distance between distributions
If we have two distributions $p, q \in \Delta^1$, the distance between them is the length of the geodesic,
\begin{equation} \label{dist} d(p, q) = \int_{q_1}^{p_1} \frac{1}{2} \frac{dt}{\sqrt{t(1-t)}} = i \ln \left(\sqrt{t} + i\sqrt{1-t}\right) \big\rvert_{q_1}^{p_1}. \end{equation}
This formula assumes $q_1 \leq p_1$; otherwise, the limits of integration need to be swapped according to the properties of the line integral. To not worry about the order of the limits of integration, one could just as well take the absolute value of the right-hand side. Upon a brief reflection, one may recognize the arccos function,
This formula, however, only works in 2D. We could derive a more general one if we stayed a little bit longer in the complex plane. Namely, substituting the limits directly in \eqref{dist},
and recognizing the $\arccos$ function afterwards, we see that
This formula, in contrast to \eqref{dist}, can be readily generalized to any finite-dimensional distributions. Denoting the standard scalar product by $\langle x, y \rangle$, the geodesic distance between distributions $p$ and $q$ can be written as
This is nothing else but the arc length on a unit sphere. To be honest, we could have stated this result immediately, since $p_i = x_i^2$ and we defined the distance on the sphere by the arc length, but it is instructive to derive it from the differentials directly.
Fisher metric is the Hessian of the KL divergence
How does the KL divergence relate to the geodesic distance? Infinitesimally, the KL looks like the Fisher metric, as was shown by Kullback in Information Theory and Statistics,
where we recognize the diagonal Hessian $H_{ii} = 1/q_i$. Comparing it with \eqref{metric}, we see that the KL divergence $KL(p\|q)$ measures the geodesic length in the vicinity of $q$,
As $p \to q$, $KL(p\|q) \to 2 d^2(p, q)$, which was pointed out by Kass and Vos in Geometrical Foundations of Asymptotic Inference. However, globally, the KL divergence
is different from the geodesic distance \eqref{geodesic}. Thus, the KL divergence is an approximation of the geodesic distance induced by the Fisher metric. It is interesting therefore to investigate how these measures of distance differ when $p$ and $q$ are far apart.
*Get rid of the proportionality constant
As a side note, if one would define the KL divergence as
then there would be no proportionality constant between $kl(q+dq\|q)$ and $h_q(dq, dq)$.
Another curious observation is that the transformation $q_i = e^{z_i}$ allows one to express the $kl$ as a differential quadratic form
in the variables $z_i = \ln q_i$.
Geodesic distance vs KL divergence
The animation below shows the KL divergence $KL(p\|q)$ and the doubled squared Fisher distance $2d^2(p, q)$ between distributions $p = [p_0, p_1]$ and $q = [q_0, q_1]$ as a function of $p_0$ for different values of $q_0$.
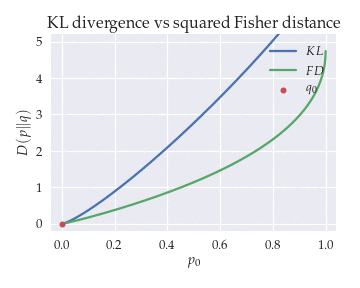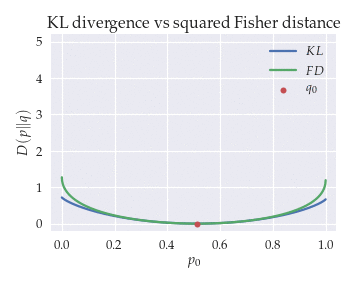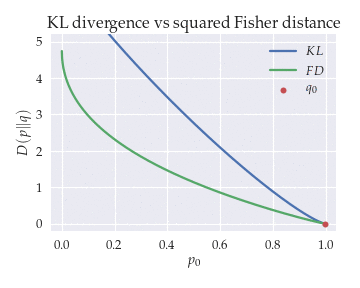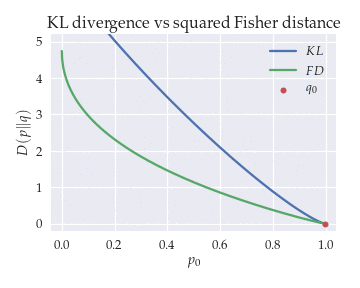
KL is a good approximation of the geodesic distance except for orthogonal distributions.
For intermediate values of $p_0$ and $q_0$, the KL divergence approximates the geodesic distance very well even if the distributions are far apart. The most noticeable difference between the KL and the Fisher distance is that the KL tends towards infinity for orthogonal distributions (i.e., when $q_0 \to 0$ and $p_0 \to 1$), whereas the Fisher distance tends towards a finite value.
Distance between Gaussians
The same reasoning can be applied to continuous distributions. Let’s try it on 1D Gaussians. The KL divergence between univariate Gaussians $p(x) = \mathcal{N}(x|\mu,1)$ and $q(x) = \mathcal{N}(x|\nu,1)$ equals
To calculate the Fisher distance \eqref{geodesic}, we need to evaluate the integral
The geodesic distance is then given by the $\arccos$ of it,
which is a more complicated function of the parameters $\mu$ and $\nu$ than the KL. Nevertheless, the KL divergence is a good upper bound on the geodesic distance, especially when the distributions are close, as the figure below shows.

Distance between Gaussians is well approximated by the KL divergence when distributions are close.
Similarly as for discrete distributions, once Gaussians are far apart, the KL grows unbounded, whereas the geodesic distance levels off. Thus, the KL divergence exagerrates the distance. For example, the KL keeps growing as we increase the distance between $\mu$ and $\nu$ despite there being almost no intersection between the densities. The geodesic distance, on the other hand, saturates after some point and reports almost no difference no matter how far apart the Gaussians are.
What consequences does quadratic growth vs saturation have in practice? In terms of optimization, the KL is preferable as it always gives a non-vanishing gradient independent of how far away the distributions are. However, the KL grows together with the $L_2$ distance between the means of the Gaussians, which may not make physical sense. Indeed, if we have samples from two Gaussians, they may lie in non-intersecting intervals of the real line. If we treat distance as a measure of distinguishability of two objects, then it should not matter how far apart the Gaussians are once samples from them do not intersect.
*Hellinger distance
returns the Euclidean distance between two points on a sphere instead of the arc length. Not surprisingly, it locally approximates the geodesic distance, because a tiny arc is indistinguishable from a line segment. However, globally, the Hellinger distance underestimates the geodesic distance, as is clear from the geometrical interpretation.